Details

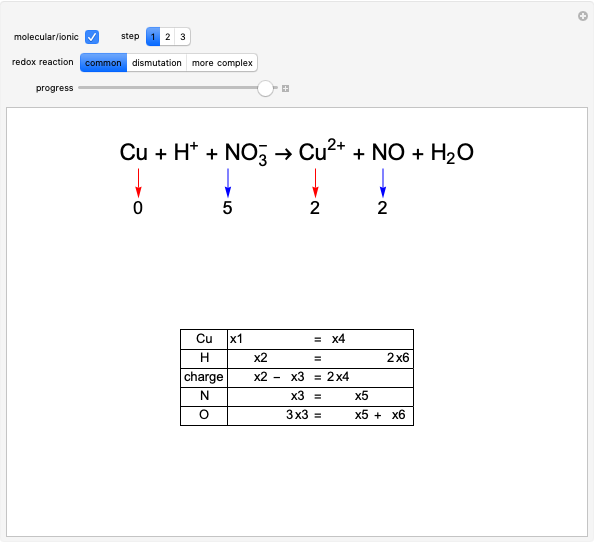
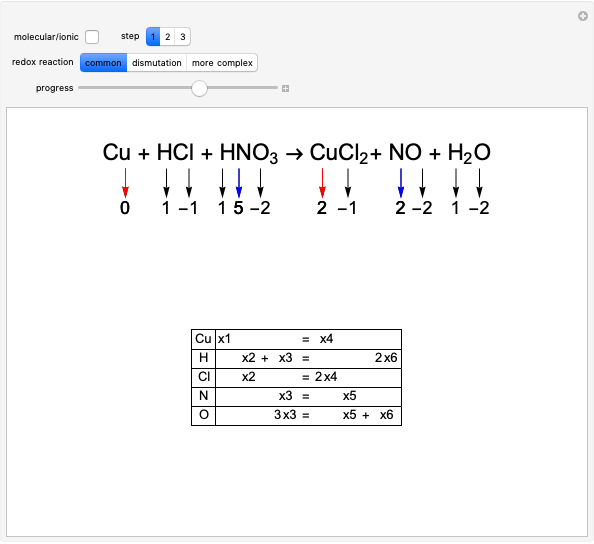
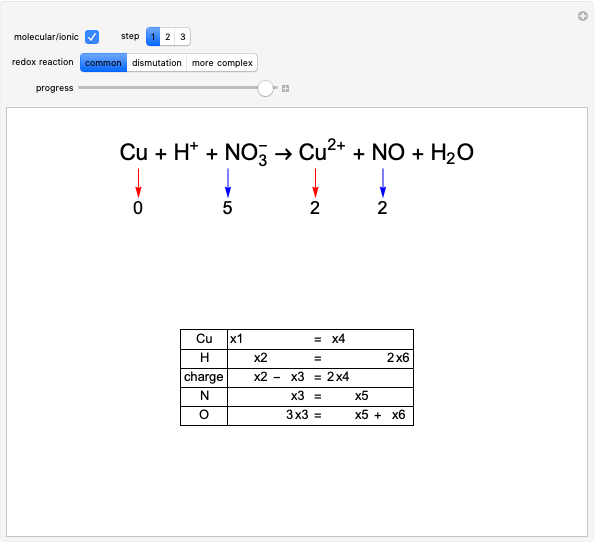
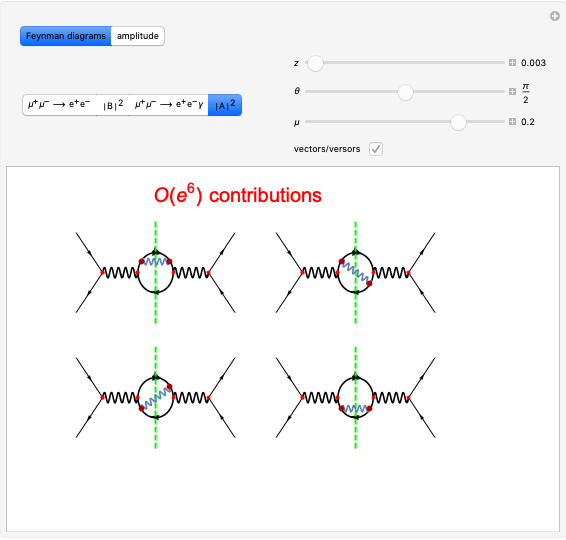
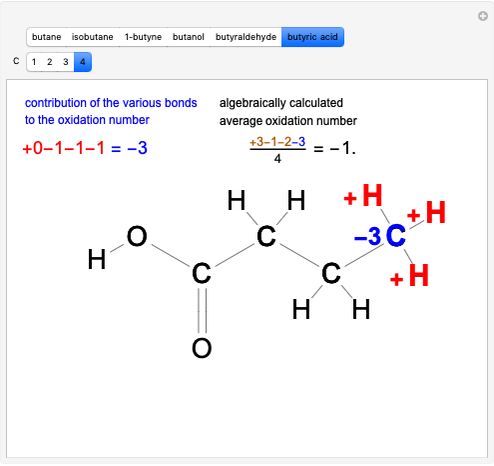
The choice "common" redox reaction refers to standard reactions either in molecular or ionic form. In step 1 the changes in oxidation number associated with two elements are highlighted: one oxidizes (reducing agent, red arrow) while the other simultaneously reduces (oxidizing agent, blue arrow).

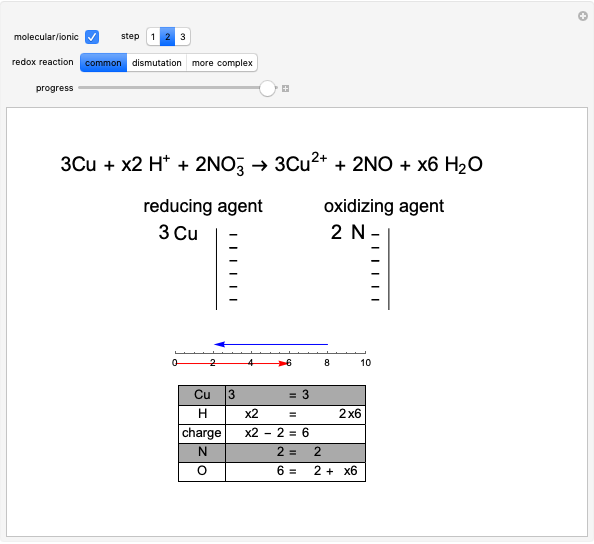
The graph on the left in step 2 shows the changes in oxidation numbers. The oxidized species (red arrow) increases the oxidation number, while the reduced species (blue arrow) decreases it. Conservation of charge is maintained.

To equalize the number of electrons given up and acquired, we calculate the minimum common multiple, thus obtaining the first four stoichiometric coefficients. Consequently, in the lower part of the window, some equations are verified, as shown by a gray background.

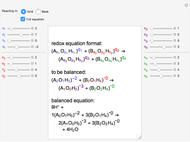
The equations with the remaining unknowns are solved in step 3 with a step-by-step procedure that involves reduction of the equations to contain just a single unknown.

After all unknowns have been determined, there remains an unused equation, which can serve as a check on the procedure.

In a "dismutation" redox reaction, also called a disproportion reaction, the same species in the reaction is both oxidized and reduced. Thereby only three stoichiometric coefficients can be calculated.

The "more complex" redox reaction considers the case when the same element (N, nitrogen with +5 as the starting oxidation number) in the reactants can be found in the product with both the same starting oxidation number (+5) and a different oxidation number (+1). The opposite case, switching reactants with products, can also occur. In both cases the coefficients set in step 2 can only be three. This eventuality occurs mainly with reactions in molecular form [1].

Snapshot 1: final part of the development of step 1, finding which oxidation numbers change

Snapshot 2: final part of the development of step 2; thanks to the equality between lost and acquired electrons, we can determine the first four stoichiometric coefficients

Snapshot 3: the remaining equation after deriving stoichiometric coefficients is used as a check

Snapshot 4: fractional stoichiometric coefficients can appear in the calculation; by an appropriate multiplication, integer coefficients can be obtained

Snapshot 5: it is common practice to omit the stoichiometric coefficient when it is equal to 1, thus in the final step it is correctly omitted

Reference

[1] S. Z. Lavagnino. Bilanciamento ossido riduzioni [Video]. (Jun 11, 2021) www.youtube.com/watch?v=U6oq6unRZMghttps://www.youtube.com/watch?v=U6oq6unRZMgNonehttps://www.youtube.com/watch?v=U6oq6unRZMgHyperlinkActionRecycledHyperlinkActiveHyperlinkRecycledHyperlinkTemplate.