Simulating the Birth-Death Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
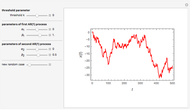
This Demonstration shows simulated paths of the simple birth-death process. Thus, you can see how the size of the population changes with time. You can adjust the initial population, the mean time between births, and the mean lifetime. The birth-death process is a special case of continuous-time Markov chains.
Contributed by: Heikki Ruskeepää (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
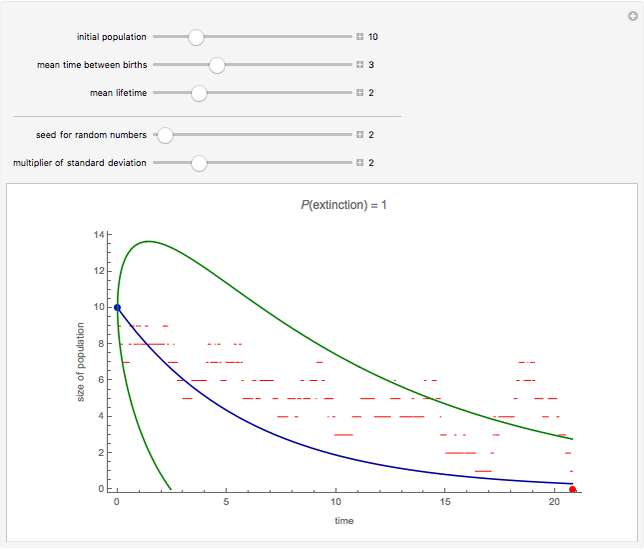
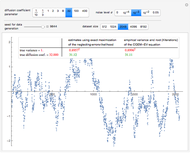
Snapshot 1: population dies out
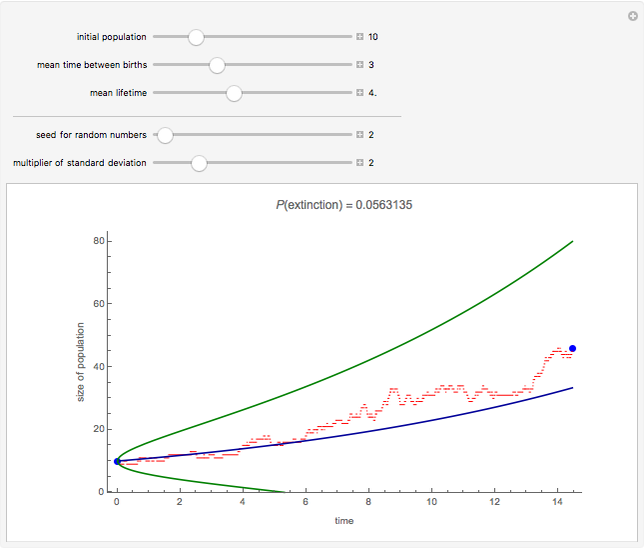
Snapshot 2: population grows
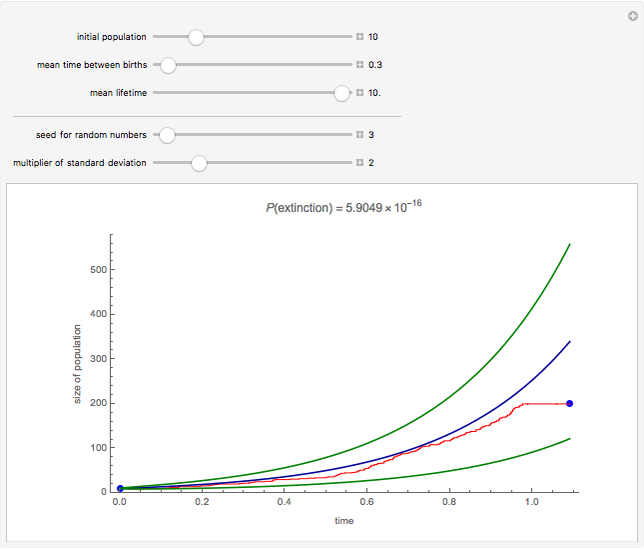
Snapshot 3: population grows above 200
In Snapshot 1, the population reaches size 0 in about 21 time units. This means that the population dies out. Extinction is expected because the mean lifetime is shorter than the mean time between births. Indeed, the probability of extinction is known to be 1 if the mean lifetime is smaller than or equal to the mean time between births. If the population dies out, the last point is red; otherwise it is blue.
In Snapshot 2, the population has a growing trend. Note that the Demonstration only shows at most the first 200 steps (births or deaths) of the process. In Snapshot 2, the 200 steps took about 15 time units.
In Snapshot 3, the population grows above 200. Note that the Demonstration only works properly if the population stays below 200. If the population reaches 200, the simulation does not allow the population to grow further.
Recall that in a birth-death process, the time between births of each individual has an exponential distribution. The lifetime of each individual has another exponential distribution. With two of the sliders, you can adjust the means of these distributions.
The blue curve is the mean of the process. The two green curves come from mean 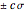 , where
, where  is the standard deviation and
is the standard deviation and  is a multiplier, controlled by a slider. The larger the value of
is a multiplier, controlled by a slider. The larger the value of  , the more likely the path stays between the two green curves.
, the more likely the path stays between the two green curves.
For the simple birth-death process, see [1, pp. 91–97]. For simulation of the simple birth-death process and other stochastic processes with Mathematica, see [2, pp. 987–1002].
[1] N. T. J. Bailey, The Elements of Stochastic Processes with Applications to the Natural Sciences, New York: Wiley, 1990.
[2] H. Ruskeepää, Mathematica Navigator: Mathematics, Statistics, and Graphics, 3rd ed., San Diego, CA: Elsevier Academic Press, 2009.
Permanent Citation
"Simulating the Birth-Death Process"
http://demonstrations.wolfram.com/SimulatingTheBirthDeathProcess/
Wolfram Demonstrations Project
Published: March 7 2011